On Third Hankel Determinant for a Subclass of Analytic Functions
[1]
Gagandeep Singh, Department of Mathematics, M. S. K. Girls College, Bharowal (Tarn-Taran), Punjab, India.
[2]
Gurcharanjit Singh, Department of Mathematics, Guru Nanak Dev University College, Chungh (Tarn-Taran), Punjab, India.
Let
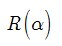
denote the class of functions analytic in the unit disc
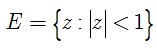
and satisfying the condition
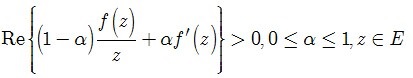
. This paper is concerned with sharp upper bound of third Hankel determinant
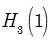
for the functions belonging to
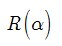
. By giving particular values to
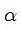
, we can easily obtain the results for different classes of functions.
Analytic Functions, Univalent Functions, Coefficient Bounds, Third Hankel Determinant
[1]
K. O. Babalola, On H3 (1) Hankel determinant for some classes of univalent functions, Inequality Theory and Applications, 6(2010), 1-7.
[2]
K. O. Babalola and T. O. Opoola, On the coefficients of certain analytic and univalent functions, Advances in Inequalities for Series, (Edited by S. S. Dragomir and A. Sofo) Nova Science Publishers, (2006), 5-17.
[3]
Aini Janteng, Suzeini Abdul Halim and Maslina Darus, Coefficient inequality for a function whose derivative has a positive real part, J. Ineq. Pure Appl. Math., 7(2) (2006), 1-5, Art. 50.
[4]
Aini Janteng, Suzeini Abdul Halim and Maslina Darus, Hankel determinant for starlike and convex functions, Int. J. Math. Anal., 1(13) (2007), 619-625.
[5]
Aini Janteng, Suzeini Abdul Halim and Maslina Darus, Hankel determinant for functions starlike and convex with respect to symmetric points, J. Quality Measurement and Anal., 2(1) (2006), 37-43.
[6]
R. J. Libera and E-J. Zlotkiewiez, Early coefficients of the inverse of a regular convex function, Proc. Amer. Math. Soc., 85(1982), 225-230.
[7]
R. J. Libera and E-J. Zlotkiewiez, Coefficient bounds for the inverse of a function with derivative in P, Proc. Amer. Math. Soc., 87(1983), 251-257.
[8]
T. H. MacGregor, Functions whose derivative has a positive real part, Trans. Amer. Math. Soc., 104(1962), 532-537.
[9]
B. S. Mehrok and Gagandeep Singh, Estimate of second Hankel determinant for certain classes of analytic functions, Scientia Magna, 8(3) (2012), 85-94.
[10]
G. Murugusundramurthi and N. Magesh, Coefficient inequalities for certain classes of analytic functions associated with Hankel determinant, Bull. Math. Anal. and Appl., 1(3)(2009), 85-89.
[11]
Ch. Pommerenke, Univalent functions, Göttingen: Vandenhoeck and Ruprecht., 1975.
[12]
G. Shanmugam, B. Adolf Stephen and K. O. Babalola, Third Hankel determinant for starlike functions, Gulf Journal of Mathematics, 2 (2) (2014), 107-113.
[13]
Gagandeep Singh, Hankel determinant for a new subclass of analytic functions, Scientia Magna, 8(4) (2012), 61-65.
[14]
Gagandeep Singh, Hankel determinant for new subclasses of analytic functions with respect to symmetric points, Int. J. of Modern Math. Sci., 5(2) (2013), 67-76.
![](https://www.facebook.com/dialog/feed?app_id=234362743428066&link=http://www.openscienceonline.com/journal/archive2?journalId=722&paperId=2353&redirect_uri=http://www.openscienceonline.com/journal/archive2?journalId=722&paperId=2353&display=popup&name=On Third Hankel Determinant for a Subclass of Analytic Functions&description=Let <img src=" http://article.openscienceonline.com/journal/722/7220186/images0001.jpg" style="border:0;"/> 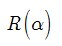denote the class of functions analytic in the unit disc 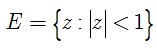<img src=" http://article.openscienceonline.com/journal/722/7220186/images0002.jpg" style="border:0;"/> and satisfying the condition 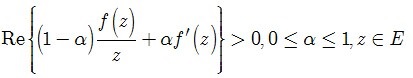<img src=" http://article.openscienceonline.com/journal/722/7220186/images0003.jpg" style="border:0;"/>. This paper is concerned with sharp upper bound of third Hankel determinant 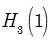<img src=" http://article.openscienceonline.com/journal/722/7220186/images0004.jpg" style="border:0;"/> for the functions belonging to 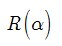<img src=" http://article.openscienceonline.com/journal/722/7220186/images0001.jpg" style="border:0;"/>. By giving particular values to 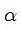<img src=" http://article.openscienceonline.com/journal/722/7220186/images0005.jpg" style="border:0;"/>, we can easily obtain the results for different classes of functions.)
